quantopian lecture random normal distribution

u is the mean

sigma is the standard deviation

sigma square is variance

class NormalRandomVariable():
    def __init__(self, mean = 0, variance = 1):
        self.variableType = "Normal"
        self.mean = mean
        self.standardDeviation = np.sqrt(variance)
        return
    def draw(self, numberOfSamples):
        samples = np.random.normal(self.mean, self.standardDeviation, numberOfSamples)
        return samples

stock1_initial = 100
R = NormalRandomVariable(0, 1)
stock1_returns = R.draw(100) # generate 100 daily returns

pd.Series(stock1_returns, name = 'stock1_return').plot()
plt.xlabel('Time')
plt.ylabel('Value');

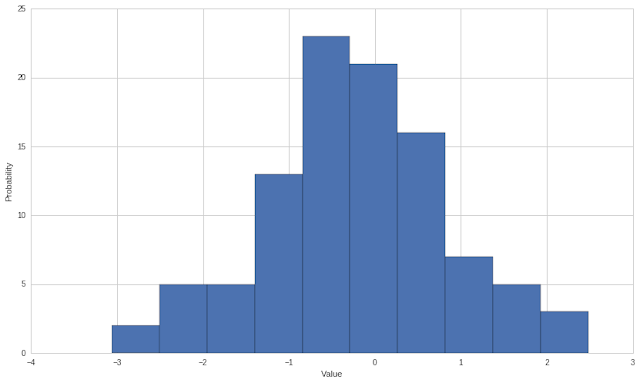
normal random daily return

plt.hist(stock1_returns, bins = 10, align = 'left')
plt.xlabel('Value')
plt.ylabel('Probability');

#accumulative returns
stock1_performance = pd.Series(np.cumsum(stock1_returns), name = 'A') + stock1_initial
stock1_performance.plot()
plt.xlabel('Time')
plt.ylabel('Value');

stock 1 performance

stock2_initial = 50

R2 = NormalRandomVariable(0, 1)

stock2_returns = R2.draw(100) # generate 100 daily returns

stock2_performance = pd.Series(np.cumsum(stock2_returns), name = 'B') + stock2_initial

stock2_performance.plot()

plt.xlabel('Time')

plt.ylabel('Value');

stock 2 performance

#assume portfolio has 50% stock1 and 50% stock2

portfolio_initial = 0.5 * stock1_initial + 0.5 * stock2_initial

portfolio_returns = 0.5 * stock1_returns + 0.5 * stock2_returns

portfolio_performance = pd.Series(np.cumsum(portfolio_returns), name = 'Portfolio') + portfolio_initial

portfolio_performance.plot()

plt.xlabel('Time')

plt.ylabel('Value');

portfolio performance

pd.concat([stock1_performance, stock2_performance, portfolio_performance], axis = 1).plot()

plt.xlabel('Time')

plt.ylabel('Value');

reference:
https://en.wikipedia.org/wiki/File:Normal_Distribution_PDF.svg
https://www.quantopian.com/lectures/random-variables