quantopian lecture linear regression

start = '2014-01-01'
end = '2015-01-01'
price = get_pricing('SPY', fields='price', start_date=start, end_date=end)

import numpy as np
from statsmodels import regression
import statsmodels.api as sm
import matplotlib.pyplot as plt
import pandas as pd

def linreg(X, Y):
    # Running the linear regression
    X = sm.add_constant(X)
    model = regression.linear_model.OLS(Y, X).fit()
    a = model.params[0]
    b = model.params[1]
    print 'slope: ', b, 'intercept: ', a
    return b, a

x = np.arange(len(price))
print x
y = price.values
slope, intercept = linreg(x, y )

[  0   1   2   3   4   5   6   7   8   9  10  11  12  13  14  15  16  17
  18  19  20  21  22  23  24  25  26  27  28  29  30  31  32  33  34  35
  36  37  38  39  40  41  42  43  44  45  46  47  48  49  50  51  52  53
  54  55  56  57  58  59  60  61  62  63  64  65  66  67  68  69  70  71
...
 198 199 200 201 202 203 204 205 206 207 208 209 210 211 212 213 214 215
 216 217 218 219 220 221 222 223 224 225 226 227 228 229 230 231 232 233
 234 235 236 237 238 239 240 241 242 243 244 245 246 247 248 249 250 251]
slope:  0.111633445889 intercept:  176.977343811

y_line = x*slope + intercept
print y_line

[ 176.97734381  177.08897726  177.2006107   177.31224415  177.42387759
  177.53551104  177.64714449  177.75877793  177.87041138  177.98204482
  178.09367827  178.20531172  178.31694516  178.42857861  178.54021205
  178.6518455   178.76347895  178.87511239  178.98674584  179.09837928
  179.21001273  179.32164617  179.43327962  179.54491307  179.65654651
  179.76817996  179.8798134   179.99144685  180.1030803   180.21471374
  180.32634719  180.43798063  180.54961408  180.66124753  180.77288097
  180.88451442  180.99614786  181.10778131  181.21941475  181.3310482
...
  200.42036745  200.53200089  200.64363434  200.75526779  200.86690123
  200.97853468  201.09016812  201.20180157  201.31343501  201.42506846
  201.53670191  201.64833535  201.7599688   201.87160224  201.98323569
  202.09486914  202.20650258  202.31813603  202.42976947  202.54140292
  202.65303637  202.76466981  202.87630326  202.9879367   203.09957015
  203.21120359  203.32283704  203.43447049  203.54610393  203.65773738
  203.76937082  203.88100427  203.99263772  204.10427116  204.21590461
  204.32753805  204.4391715   204.55080495  204.66243839  204.77407184
  204.88570528  204.99733873]
 
line = pd.Series(y_line, index=price.index, name='linear fit')
 
pd.concat([r_b, line], axis = 1).plot()
plt.xlabel('Time')
plt.ylabel('Value');

reference:
https://www.quantopian.com/lectures/linear-regression
https://www.quantopian.com/lectures/regression-model-instability
https://docs.scipy.org/doc/numpy/reference/generated/numpy.arange.html
https://www.statsmodels.org/dev/generated/statsmodels.regression.linear_model.OLS.html

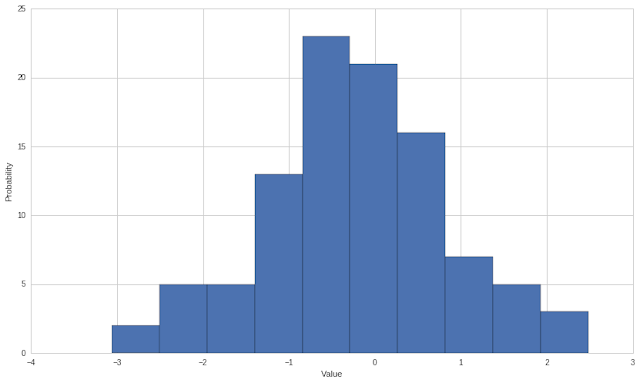
quantopian lecture random normal distribution

u is the mean

sigma is the standard deviation

sigma square is variance

class NormalRandomVariable():
    def __init__(self, mean = 0, variance = 1):
        self.variableType = "Normal"
        self.mean = mean
        self.standardDeviation = np.sqrt(variance)
        return
    def draw(self, numberOfSamples):
        samples = np.random.normal(self.mean, self.standardDeviation, numberOfSamples)
        return samples

stock1_initial = 100
R = NormalRandomVariable(0, 1)
stock1_returns = R.draw(100) # generate 100 daily returns

pd.Series(stock1_returns, name = 'stock1_return').plot()
plt.xlabel('Time')
plt.ylabel('Value');

normal random daily return

plt.hist(stock1_returns, bins = 10, align = 'left')
plt.xlabel('Value')
plt.ylabel('Probability');

#accumulative returns
stock1_performance = pd.Series(np.cumsum(stock1_returns), name = 'A') + stock1_initial
stock1_performance.plot()
plt.xlabel('Time')
plt.ylabel('Value');

stock 1 performance

stock2_initial = 50

R2 = NormalRandomVariable(0, 1)

stock2_returns = R2.draw(100) # generate 100 daily returns

stock2_performance = pd.Series(np.cumsum(stock2_returns), name = 'B') + stock2_initial

stock2_performance.plot()

plt.xlabel('Time')

plt.ylabel('Value');

stock 2 performance

#assume portfolio has 50% stock1 and 50% stock2

portfolio_initial = 0.5 * stock1_initial + 0.5 * stock2_initial

portfolio_returns = 0.5 * stock1_returns + 0.5 * stock2_returns

portfolio_performance = pd.Series(np.cumsum(portfolio_returns), name = 'Portfolio') + portfolio_initial

portfolio_performance.plot()

plt.xlabel('Time')

plt.ylabel('Value');

portfolio performance

pd.concat([stock1_performance, stock2_performance, portfolio_performance], axis = 1).plot()

plt.xlabel('Time')

plt.ylabel('Value');

reference:
https://en.wikipedia.org/wiki/File:Normal_Distribution_PDF.svg
https://www.quantopian.com/lectures/random-variables

quantopian lecture discrete random binomial distribution - Pachinko game

Pachinko game

ball has equal chance to move right or left when hit obstacle

program simulates the distribution of balls when they fall to the bottom slots

class BinomialRandomVariable():
    def __init__(self, slots = 10, probabilityMovingRight = 0.5):
        self.variableType = "Binomial"
        self.slots = slots
        self.probabilityMovingRight = probabilityMovingRight
        return
    def draw(self, numberOfBalls):
        distribution = np.random.binomial(self.slots, self.probabilityMovingRight, numberOfBalls)
        return distribution

#10 slots, chance of moving right when hit obstacle is 50%, 1000 balls fall from top  
data = BinomialRandomVariable(10, 0.50).draw(1000)
print data

plt.hist(data, bins=21)
plt.xlabel('Value')
plt.ylabel('Occurences');

[ 7  5  5  4  3  4  2  5  5  5  6  4  4  5  4  6  5  3  3  4  6  4  4  6  6
  3  4  5  5  5  1  4  5  4  7  5  6  6  4  8  6  5  3  6  6  5  8  4  3  4
  4  6  6  7  7  9  5  4  6  4  4  5  7  3  6  6  5  3  5  3  0  4  2  6  3
  1  2  7  3  3  7  6  5  5  4  5  3  5  4  7  4  2  6  6  4  2  5  6  3  7
  6  6  4  6  2  7  6  7  5  6  5  5  4  4  2  2  7  6  5  4  5  6  9  5  3
  5  2  4  4  4  4  3  5  6  6  3  6  6  5  3  7  6  6  2  4  6  6  3  4  4
  7  6  8  4  5  2  6  4  3  4  7  6  5  5  4  7  7  4  4  5  2  3  6  5  6
  1  5  4  7  4  5  3  3  2  5  4  3  2  6  8  6  4  6  5  5  2  3 10  3  5
  3  6  4  4  4  6  6  5  5  5  3  8  4  6  4  8  6  6  7  6  9  3  5  2  4
  4  5  6  9  5  2  6  8  6  5  5  3  4  2  1  7  7  4  5  6  3  4  7  4  3
  6  9  7  7  3  5  4  4  3  2  5  7  5  8  7  6  5  2  5  3  4  4  6  3  7
  3  5  6  3  5  6  8  4  5  7  4  6  6  4  6  7  5  9  5  2  4  5  2  2  5
  4  6  7  4  5  6  6  6  7  8  7  3  4  6  4  4  6  5  3  6  6  6  5  1  5
  3  4  8  8  4  6  5  3  3  6  7  2  3  6  6  4  5  5  6  7  8  5  4  7  6
  3  3  5  5  3  5  4  5  4  8  6  4  6  5  4  6  6  6  5  5  7  3  4  3  6
  5  6  6  7  5  5  6  4  5  6  5  4  7  5  5  3  5  6  4  6  4  5  3  7  4
  8  3  5  4  3  4  5  5  6  4  6  5  7  4  4  5  4  3  6  6  6  4  6  6  4
  6  7  3  5  5  7  7  4  8  4  8  6  5  7  3  3  6  6  6  6  5  4  8  3  6
  5  6  5  4  5  8  2  4  3  5  5  5  4  4  6  5  5  6  8  4  5  6  6  3  3
  5  6  6  4 10  5  4  6  5  4  6  6  6  3  5  5  6  5  4  7  7  4  4  2  5
  4  6  8  4  6  5  5  4  3  7  4  1  2  4  5  5  2  6  4  7  7  7  2  4  5
  4  6  7  5  6  5  4  2  5  5  6  6  4  4  5  6  7  4  8  3  4  6  5  6  0
  5  5  4  5  8  6  7  3  4  4  3  5  6  6  6  4  5  2  7  7  6  6  5  5  5
  4  4  5  4  4  6  4  5  5  5  5  3  2  4  5  3  7  4  6  3  6  1  2  4  6
  5  5  5  7  4  4  5  7  3  5  5  4  6  2  5  7  6  3  7  5  4  3  3  6  3
  3  4  5  7  4  6  4  5  4  5  6  5  7  7  7  7  4  4  5  6  8  1  3  6  5
  3  5  2  3  7  4  5  7  3  4  5  4  4  5  6  6  6  5  3  5  5  6  5  5  2
  6  6  7  6  3  5  6  5  2  7  4  4  5  5  6  4  8  8  4  4  6  7  4  2  7
  7  5  4  4  5  6  3  5  5  4  6  3  6  7  6  3  6  8  5  4  4  6  6  4  6
  3  4  7  6  8  3  4  4  8  5  7  5  5  5  3  5  4  2  5  6  5  6  8  2  4
  3  6  4  4  6  7  3  4  6  7  4  5  5  2  6  3  4  5  3  5  8  8  7  4  5
  2  6  7  6  5  4  4  5  9  9  7  4  5  4  3  4  4  4  5  6  9  2  6  4  6
  5  6  4  5  7  7  6  3  3  3  5  7  7  8  5  7  6  5  4  7  5  5  4  4  7
  6  7  5  4  5  5  6  4  7  2  7  8  3  5  4  5  2  6  3  4  5  5  5  8  3
  6  4  4  5  6  6  4  6  5  8  7  5  5  7  3  6  5  4  6  7  6  2  4  3  5
  4  4  3  3  4  6  6  4  7  3  4  5  6  4  7  4  5  4  4  4  6  3  8  5  5
  5  5  4  7  3  3  3  5  6  5  5  5  4  5  4  4  6  4  7  3  4  5  5  6  5
  4  5  5  5  3  5  5  7  3  7  6  6  5  5  6  4  4  3  3  3  4  8  2  4  5
  3  6  4  2  3  6  2  6  5  5  4  5  5  6  6  5  4  7  5  5  2  4  5  3  4
  8  4  6  7  2  4  4  3  4  7  3  7  7  4  2  5  5  6  7  6  5  1  3  4  4]

balls fall mostly to the middle slots

#simulate balls turn to move left when hit obstacle

#10 slots, chance of moving right when hit obstacle is 35%, 1000 balls fall from top  

data = BinomialRandomVariable(10, 0.35).draw(1000)

[3 2 4 6 4 2 1 6 3 4 2 3 4 1 3 3 6 4 3 7 4 5 3 3 5 4 5 3 5 2 2 4 3 4 2 7 2
 5 3 3 3 2 6 3 2 2 2 3 4 4 3 6 3 2 3 4 5 2 1 6 6 1 2 2 5 3 6 7 6 3 5 7 5 4
 3 3 5 5 4 4 6 2 3 3 3 2 4 3 6 3 5 3 2 4 4 3 3 5 4 1 4 5 3 4 4 6 7 4 2 4 3
 4 3 4 4 3 5 4 4 5 2 3 6 5 4 4 4 5 6 3 1 1 4 2 3 6 3 2 4 3 2 2 2 3 2 5 5 4
 2 2 4 3 2 2 3 2 4 4 3 3 3 4 4 3 3 2 3 4 5 4 1 3 1 2 2 2 3 7 1 2 3 4 2 2 5
 2 4 3 5 1 5 3 3 4 2 3 2 2 6 1 2 1 5 3 2 5 6 4 2 5 1 2 3 3 4 4 4 1 3 3 4 0
 1 2 2 4 3 4 4 6 2 3 3 5 5 4 5 3 2 4 2 3 3 1 5 2 3 3 4 3 5 6 5 4 3 5 6 3 3
 3 4 2 3 2 4 2 3 4 3 3 2 6 3 2 0 3 3 4 3 4 4 2 2 6 4 4 2 2 4 3 5 5 2 2 4 6
 1 3 4 5 3 3 2 4 4 2 1 3 4 3 3 1 0 5 3 4 5 2 4 2 3 2 5 0 2 3 3 2 2 1 6 6 1
 3 4 5 4 3 6 4 5 5 3 1 4 2 4 4 2 3 5 4 4 1 5 6 3 7 5 3 4 6 3 2 6 2 4 3 3 6
 1 3 3 5 2 7 3 4 2 6 2 4 5 7 3 5 4 2 3 2 3 3 2 1 4 3 1 5 2 2 5 2 3 3 4 2 3
 3 6 4 1 3 7 1 3 4 4 2 3 4 4 2 6 3 4 2 2 3 3 3 2 4 2 2 5 2 5 4 1 3 4 4 3 2
 5 4 4 4 4 4 5 4 3 2 3 2 5 5 2 4 6 2 1 2 4 5 3 3 5 5 4 3 3 6 4 4 5 3 2 3 4
 4 3 1 5 7 3 2 4 4 3 3 5 4 3 1 2 6 3 4 3 4 6 6 6 2 4 2 3 6 3 3 2 3 7 2 6 1
 2 3 5 5 4 2 2 1 3 4 7 5 3 1 3 4 4 4 3 5 2 1 4 1 4 4 5 2 2 3 5 6 5 3 1 4 4
 4 5 4 3 3 5 6 5 6 3 2 5 3 2 4 2 4 4 3 1 5 5 3 5 3 2 2 4 6 4 3 6 3 3 4 3 3
 4 3 2 4 5 4 2 2 3 7 3 4 3 3 5 5 1 5 4 6 4 2 3 5 3 4 4 1 2 3 3 4 5 1 4 3 4
 2 3 7 2 3 3 2 3 3 3 6 5 3 3 4 4 3 3 3 3 1 3 3 6 5 4 3 4 4 2 3 3 6 3 2 4 4
 4 4 3 3 3 2 4 2 4 4 3 3 0 4 3 2 5 6 3 2 3 3 4 1 4 6 4 5 5 3 4 5 2 6 3 4 2
 3 2 4 2 5 4 3 3 2 4 4 1 4 4 5 4 0 3 5 5 5 4 5 3 3 4 3 3 2 3 5 4 8 3 4 1 5
 4 2 5 2 2 8 1 2 5 6 5 3 6 3 3 7 6 4 2 5 4 4 3 5 3 5 3 4 1 3 5 4 2 4 2 3 3
 4 2 3 3 5 4 3 2 3 2 1 2 4 4 1 2 3 6 5 5 4 6 2 5 6 2 2 5 2 2 2 8 3 6 1 3 4
 2 4 2 5 4 3 2 3 2 3 5 2 4 1 6 4 6 5 4 8 3 3 5 2 2 4 2 5 2 3 3 2 3 3 3 5 4
 4 5 2 2 3 4 5 3 3 3 3 3 6 4 3 2 2 7 4 5 6 2 3 4 5 2 4 3 1 4 4 3 3 3 3 4 7
 4 3 2 4 4 2 2 3 4 1 2 2 5 1 3 2 3 3 3 5 4 4 4 4 3 3 5 5 1 5 7 3 4 4 4 3 2
 6 3 2 3 2 3 6 4 1 3 3 3 4 3 5 5 2 2 2 4 4 3 3 3 5 2 5 4 4 3 5 2 2 5 2 3 3
 4 2 2 5 5 2 4 3 5 4 3 4 1 1 4 2 2 1 3 4 2 3 5 8 5 4 1 2 2 3 5 3 4 3 3 0 3
 6]

balls concentrate on left slots, no ball falls in very right slot 10

reference:

https://arxiv.org/pdf/1601.05706.pdf

https://www.quantopian.com/lectures/random-variables

quantopian lecture discrete random uniform distribution

import numpy as np
import pandas as pd
import matplotlib.pyplot as plt

class DiscreteRandomVariable:
    def __init__(self, a=0, b=1):
        self.variableType = ""
        self.low = a
        self.high = b
        return
    def draw(self, numberOfSamples):
        samples = np.random.randint(self.low, self.high, numberOfSamples)
        return samples
 
DieRolls = DiscreteRandomVariable(1, 6)
data = DieRolls.draw(10)
print data

plt.hist(data, bins=20)
plt.xlabel('Value')
plt.ylabel('Occurences')
plt.legend(['Die Rolls']);

[3 2 5 4 6 5 1 3 6 2]

histogram shows how many times dice rests on each face during 10 rolls.

[6 1 1 6 3 1 2 6 3 4]

try another 10 rolls, results are very different

[4 4 1 4 4 4 5 4 1 6 3 4 6 2 5 1 4 1 2 5 5 5 1 2 1 3 4 5 2 4 2 4 2 3 4 4 2
 4 4 2 6 1 4 5 3 1 2 4 6 2 2 6 3 5 5 3 1 1 1 5 6 3 4 6 5 4 5 4 3 2 4 3 1 1
 5 2 5 5 2 5 4 5 4 4 5 5 2 3 2 1 5 6 1 5 2 2 4 6 6 4 3 6 2 4 4 5 4 6 5 2 2
 4 4 4 5 1 3 5 3 4 2 6 3 3 6 2 5 4 6 3 2 3 4 2 1 1 1 4 1 5 1 1 4 1 6 4 6 6
 4 2 5 1 6 6 6 1 6 5 1 2 2 5 3 6 2 4 6 1 3 4 4 4 6 5 4 2 2 6 1 1 6 6 6 5 4
 3 1 2 6 2 1 3 2 2 4 2 2 1 1 2 3 5 5 6 5 3 4 4 5 1 1 2 5 4 5 4 5 1 2 5 1 5
 4 6 1 3 3 3 3 5 6 6 6 5 6 2 3 6 4 6 3 6 6 3 5 2 2 4 1 4 1 3 5 2 1 4 2 3 1
 2 1 5 2 2 1 3 2 3 5 4 2 1 2 1 1 5 2 2 6 5 2 6 6 5 6 6 4 1 3 5 5 6 1 1 6 6
 6 3 5 1 3 3 1 5 5 6 5 5 4 3 1 4 3 1 6 5 4 5 2 4 2 2 2 1 1 2 1 5 3 4 4 4 5
 4 5 6 5 1 4 1 2 4 3 1 3 6 3 5 6 1 5 5 6 3 6 2 6 2 5 5 1 4 3 2 3 3 2 4 1 1
 5 3 3 3 3 2 5 2 1 6 6 6 5 2 2 5 5 6 3 5 6 6 3 1 6 1 5 2 3 6 1 5 4 2 3 6 3
 5 5 6 5 2 6 1 3 2 6 6 1 1 1 2 6 1 1 4 2 6 5 5 4 4 5 5 3 1 2 3 4 6 5 6 3 6
 2 2 4 4 3 1 3 5 4 6 4 6 6 5 4 4 3 1 6 3 2 5 5 5 3 2 6 2 2 4 3 4 5 1 5 3 1
 5 3 2 3 1 5 3 1 2 5 2 6 4 3 5 4 5 3 1 1 6 4 1 5 4 1 5 4 2 3 2 4 2 2 1 6 3
 6 4 1 2 4 5 3 2 4 5 1 3 2 2 1 4 5 2 5 2 5 2 5 1 2 1 2 5 2 1 6 4 5 6 2 6 3
 5 2 1 6 6 5 2 2 6 2 4 4 5 5 1 2 5 5 5 3 2 3 5 1 6 1 1 3 1 1 3 5 3 3 4 3 4
 1 5 2 6 6 5 4 5 4 6 5 2 2 5 3 6 6 4 2 5 5 3 6 5 3 2 4 5 4 4 2 2 2 4 3 3 3
 1 2 4 6 6 6 5 4 6 1 5 5 3 5 4 1 3 4 6 2 5 2 2 6 1 2 2 4 2 3 2 6 5 2 3 5 2
 6 4 2 6 3 6 1 4 6 5 5 1 4 1 1 6 5 3 1 6 1 3 2 6 5 1 2 1 6 4 1 3 3 5 6 5 3
 4 3 5 3 6 3 4 4 3 2 6 5 1 2 1 4 6 2 3 1 5 6 4 2 1 2 3 1 5 6 3 4 5 6 3 4 1
 2 6 2 5 3 6 4 6 3 1 5 5 5 5 3 5 5 5 1 4 4 4 6 1 3 1 2 3 3 3 6 6 6 6 3 5 1
 1 4 4 1 3 3 6 4 2 5 6 5 3 6 2 4 1 4 2 6 4 3 2 3 6 5 2 1 3 6 5 4 6 2 4 1 6
 3 6 6 5 5 2 4 3 2 6 1 2 5 6 3 4 1 2 5 2 5 3 6 1 5 2 6 4 6 6 6 6 5 2 4 2 1
 5 3 3 2 2 2 6 6 5 4 6 5 5 2 5 1 5 1 3 1 1 4 4 3 4 2 1 5 2 2 3 4 5 6 4 3 4
 1 3 4 6 1 1 3 4 2 6 6 4 4 2 6 4 5 3 4 1 4 2 4 5 6 3 6 1 6 2 6 1 5 6 1 2 3
 1 3 2 3 6 2 1 4 4 4 2 6 3 3 4 6 2 3 4 4 2 4 1 5 1 5 6 3 4 1 1 2 5 6 3 1 3
 5 1 1 3 5 2 2 2 5 6 6 3 4 4 4 1 3 4 4 5 5 3 2 6 6 1 4 5 5 3 4 4 2 1 6 3 3
 4]

try roll 1000 times, dice almost has uniform chance to rest on each face

quantopian lecture rolling mean, rolling std

import numpy as np
import pandas as pd
import matplotlib.pyplot as plt

start = '2018-01-01'
end = '2019-02-01'
data = get_pricing(['MSFT'], fields='price', start_date=start, end_date=end)

rm = data.rolling(window=30,center=False).mean()
std = data.rolling(window=30,center=False).std()

_, ax = plt.subplots()
ax.plot(data.index, data)
ax.plot(rm.index, rm)
ax.plot(rm + std)
ax.plot(rm - std)

plt.title("Mcrosoft Prices")
plt.ylabel("Price")
plt.xlabel("Date");
plt.legend(['Price', 'Moving Average', 'Moving Average +1 Std', 'Moving Average -1 Std'])

#rolling standard  deviation is not a constant
print std

2018-02-13 00:00:00+00:00             2.561080
...                                        ...
2018-12-19 00:00:00+00:00             2.896930
2018-12-20 00:00:00+00:00             3.068813
2018-12-21 00:00:00+00:00             3.353129
2018-12-24 00:00:00+00:00             3.949504
2018-12-26 00:00:00+00:00             4.022458
2018-12-27 00:00:00+00:00             4.104846
2018-12-28 00:00:00+00:00             4.207010
2018-12-31 00:00:00+00:00             4.260755
2019-01-02 00:00:00+00:00             4.307897
2019-01-03 00:00:00+00:00             4.482073
2019-01-04 00:00:00+00:00             4.510192
2019-01-07 00:00:00+00:00             4.502924
2019-01-08 00:00:00+00:00             4.506345
2019-01-09 00:00:00+00:00             4.497546
2019-01-10 00:00:00+00:00             4.487874
2019-01-11 00:00:00+00:00             4.470221
2019-01-14 00:00:00+00:00             4.303732
2019-01-15 00:00:00+00:00             4.151837
2019-01-16 00:00:00+00:00             3.947878
2019-01-17 00:00:00+00:00             3.652218
2019-01-18 00:00:00+00:00             3.616924
2019-01-22 00:00:00+00:00             3.484868
2019-01-23 00:00:00+00:00             3.531261
2019-01-24 00:00:00+00:00             3.485831
2019-01-25 00:00:00+00:00             3.421721

Laurentian bank 3.3% saving interest

LBC Digital High Interest Savings Account*

Since 2003, Laurentian Bank has been available only in Quebec, but with the recent launch of a new digital offering at LBCDigital.ca, the institution is tempting clients from across the country. The headline news is a rate of 3.30% in their high interest savings account with no minimum balance and no monthly fees, easily topping most financial institutions’ best rates on GICs, which lock in your money for a specified period of time. With the LBC Digital High Interest Savings Account, you can access funds whenever you like, and frequently used services including electronic fund transfers, pre-authorized deposits, and transfers between LBC Digital accounts are included. This last is important as it means you can move your money to an LBCDigital.ca chequing account, from which you can make unlimited free Interac e-Transfers.

Promotions: None
Interest rate: 3.30%
Minimum balance: None
Free transactions per month: Unlimited
Fee for Interac e-Transfers: Free
Fees for extras: None
CDIC insured: Eligible on deposits up to $100,000 in Canadian funds that are payable in Canada and have a term of no more than 5 years
Other restrictions: Non-sufficient funds (NSF), returned items, and overdrawn accounts are subject to fees, and if you close the account within 90 days there is a $25 penalty

The bank merged with Eaton Trust Company (in 1988), purchased Standard Trust's assets (1991), acquired La Financière Coopérants Prêts-Épargne Inc., and Guardian Trust Company in Ontario (1992), acquired General Trust Corporation in Ontario, and purchased some Société Nationale de Fiducie assets and the brokerage firm BLC Rousseau (1993).

In 1993, the Desjardins-Laurentian Financial Corporation became the new majority shareholder of Laurentian Bank of Canada, following the merging of the Laurentian Group Corporation with the Desjardins Group. The bank purchased the Manulife Bank of Canada’s banking service network and the assets of Prenor Trust Company of Canada in 1994.

In 1995, the bank acquired 30 branches of the North American Trust Company.

In 1996, one of its subsidiaries acquired the parent corporation of Trust Prêt et Revenu du Canada. A few months later, the withdrawal of its main shareholder, Desjardins-Laurentian Financial Corporation, prompted the Laurentian Bank to become a Schedule 1 Bank under the Bank Act, on par with all the other large Canadian banks.

reference:
https://www.moneysense.ca/save/best-high-interest-savings-accounts-canada/
https://en.wikipedia.org/wiki/Laurentian_Bank_of_Canada
https://en.wikipedia.org/wiki/List_of_banks_and_credit_unions_in_Canada
https://www.lbcdigital.ca/en/saving/high-interest-savings-account?gclid=CjwKCAiAlO7uBRANEiwA_vXQ-25d4o1mQ6wrFQwChzXyVK8HcuP41eYeQRl8yw5TGDY3YW4A61XecBoCNgMQAvD_BwE&gclsrc=aw.ds

quantopian lecture mean, standard deviation

A low standard deviation indicates that the values tend to be close to the mean of the set, while a high standard deviation indicates that the values are spread out over a wider range.

import numpy as np
import matplotlib.pyplot as plt

start = '2018-01-01'
end = '2019-02-01'
data = get_pricing(['MSFT'], fields='price', start_date=start, end_date=end)

_, ax = plt.subplots()

mean = data.mean().values
std = data.std().values

ax.plot(data.index, data)
ax.axhline(mean)
ax.axhline(mean + std, linestyle='--')
ax.axhline(mean - std, linestyle='--')

plt.title("Mcrosoft Prices")
plt.ylabel("Price")
plt.xlabel("Date");
plt.legend(['stock price', 'Mean', '+/- 1 Standard Deviation'])

reference:
https://www.quantopian.com/lectures/instability-of-estimates
https://en.wikipedia.org/wiki/Standard_deviation

quantopian lecture histogram

import numpy as np
import matplotlib.pyplot as plt

start = '2019-01-01'
end = '2019-11-20'
data = get_pricing(['AAPL', 'MSFT'], fields='price', start_date=start, end_date=end)

data.columns = [e.symbol for e in data.columns]

data['AAPL'].plot();
plt.title("Apple Prices")
plt.ylabel("Price")
plt.xlabel("Date");

#price histogram - how many days stock is at certain price during 2019
plt.hist(data['AAPL'], bins=20)
plt.xlabel('Price')
plt.ylabel('Number of Days Observed')
plt.title('Frequency Distribution of AAPL Prices, 2019');

#return histogram - how many days stock performs daily in certain percentage
R = data['AAPL'].pct_change()[1:]

plt.hist(R, bins=20)
plt.xlabel('Percent Return in a day')
plt.ylabel('Number of Days Observed')
plt.title('Frequency Distribution of AAPL Returns, 2019');

quantopian lecture pandas 2

import numpy as np
import pandas as pd
import matplotlib.pyplot as plt

dict_data = {
    'a' : [1, 2, 3, 4, 5],
    'b' : ['L', 'K', 'J', 'M', 'Z'],
    'c' : np.random.normal(0, 1, 5)
}

frame_data = pd.DataFrame(dict_data, index=pd.date_range('2016-01-01', periods=5))
print frame_data

            a  b         c
2016-01-01  1  L  1.244900
2016-01-02  2  K -0.342299
2016-01-03  3  J  0.622280
2016-01-04  4  M  0.568443
2016-01-05  5  Z -1.024938

s_1 = pd.Series([2, 4, 6, 8, 10], name='Evens')
s_2 = pd.Series([1, 3, 5, 7, 9], name="Odds")
numbers = pd.concat([s_1, s_2], axis=1)
print numbers
numbers.columns = ['Shmevens', 'Shmodds']
print numbers
numbers.index = pd.date_range("2016-01-01", periods=len(numbers))
print numbers
numbers.values

   Evens  Odds
0      2     1
1      4     3
2      6     5
3      8     7
4     10     9
   Shmevens  Shmodds
0         2        1
1         4        3
2         6        5
3         8        7
4        10        9
            Shmevens  Shmodds
2016-01-01         2        1
2016-01-02         4        3
2016-01-03         6        5
2016-01-04         8        7
2016-01-05        10        9
array([[ 2,  1],
       [ 4,  3],
       [ 6,  5],
       [ 8,  7],
       [10,  9]])

symbol = ["CMG", "MCD", "SHAK", "WFM"]
start = "2012-01-01"
end = "2016-01-01"
prices = get_pricing(symbol, start_date=start, end_date=end, fields="price")
prices.columns = map(lambda x: x.symbol, prices.columns)

prices.loc[:, 'CMG'].head()
2012-01-03 00:00:00+00:00    340.980
2012-01-04 00:00:00+00:00    348.740
2012-01-05 00:00:00+00:00    349.990
2012-01-06 00:00:00+00:00    348.950
2012-01-09 00:00:00+00:00    339.522
Freq: C, Name: CMG, dtype: float64

prices.loc[:, ['CMG', 'MCD']].head()
CMG MCD
2012-01-03 00:00:00+00:00 340.980 86.631
2012-01-04 00:00:00+00:00 348.740 87.166
2012-01-05 00:00:00+00:00 349.990 87.526
2012-01-06 00:00:00+00:00 348.950 88.192
2012-01-09 00:00:00+00:00 339.522 87.342

prices.loc['2015-12-15':'2015-12-22']
CMG MCD SHAK WFM
2015-12-15 00:00:00+00:00 555.64 116.96 41.510 32.96
2015-12-16 00:00:00+00:00 568.50 117.85 40.140 33.65
2015-12-17 00:00:00+00:00 554.91 117.54 38.500 33.38
2015-12-18 00:00:00+00:00 541.08 116.58 39.380 32.72
2015-12-21 00:00:00+00:00 521.71 117.70 38.205 32.98
2015-12-22 00:00:00+00:00 495.41 117.71 39.760 34.79

prices.loc['2015-12-15':'2015-12-22', ['CMG', 'MCD']]
CMG MCD
2015-12-15 00:00:00+00:00 555.64 116.96
2015-12-16 00:00:00+00:00 568.50 117.85
2015-12-17 00:00:00+00:00 554.91 117.54
2015-12-18 00:00:00+00:00 541.08 116.58
2015-12-21 00:00:00+00:00 521.71 117.70
2015-12-22 00:00:00+00:00 495.41 117.71

# Access prices with integer index in
# [1, 3, 5, 7, 9, 11, 13, ..., 99]
# and in column 0 or 3
prices.iloc[range(1, 100, 2), [0, 3]].head(20)
CMG WFM
2012-01-04 00:00:00+00:00 348.74 33.650
2012-01-06 00:00:00+00:00 348.95 34.319
2012-01-10 00:00:00+00:00 340.70 34.224
2012-01-12 00:00:00+00:00 347.83 33.913
2012-01-17 00:00:00+00:00 353.61 36.230
2012-01-19 00:00:00+00:00 358.10 36.489
2012-01-23 00:00:00+00:00 360.53 35.918
2012-01-25 00:00:00+00:00 363.28 36.404
2012-01-27 00:00:00+00:00 366.80 35.338
2012-01-31 00:00:00+00:00 367.58 34.932
2012-02-02 00:00:00+00:00 362.64 35.673
2012-02-06 00:00:00+00:00 371.65 36.055
2012-02-08 00:00:00+00:00 373.81 36.768
2012-02-10 00:00:00+00:00 376.39 38.509
2012-02-14 00:00:00+00:00 379.14 38.216
2012-02-16 00:00:00+00:00 381.91 38.032
2012-02-21 00:00:00+00:00 383.86 38.018
2012-02-23 00:00:00+00:00 386.82 38.240
2012-02-27 00:00:00+00:00 389.11 38.528
2012-02-29 00:00:00+00:00 390.47 38.098

#boolean index
prices.loc[prices.MCD > prices.WFM].head()
CMG MCD SHAK WFM
2012-01-03 00:00:00+00:00 340.980 86.631 NaN 32.788
2012-01-04 00:00:00+00:00 348.740 87.166 NaN 33.650
2012-01-05 00:00:00+00:00 349.990 87.526 NaN 34.257
2012-01-06 00:00:00+00:00 348.950 88.192 NaN 34.319
2012-01-09 00:00:00+00:00 339.522 87.342 NaN 34.323

prices.loc[(prices.MCD > prices.WFM) & ~prices.SHAK.isnull()].head()
CMG MCD SHAK WFM
2015-01-30 00:00:00+00:00 709.58 89.331 45.76 51.583
2015-02-02 00:00:00+00:00 712.69 89.418 43.50 52.623
2015-02-03 00:00:00+00:00 726.07 90.791 44.87 52.880
2015-02-04 00:00:00+00:00 675.99 90.887 41.32 53.138
2015-02-05 00:00:00+00:00 670.57 91.177 42.46 52.851

#add column
s_1 = get_pricing('TSLA', start_date=start, end_date=end, fields='price')
prices.loc[:, 'TSLA'] = s_1
prices.head(5)
CMG MCD SHAK WFM TSLA
2012-01-03 00:00:00+00:00 340.980 86.631 NaN 32.788 28.06
2012-01-04 00:00:00+00:00 348.740 87.166 NaN 33.650 27.71
2012-01-05 00:00:00+00:00 349.990 87.526 NaN 34.257 27.12
2012-01-06 00:00:00+00:00 348.950 88.192 NaN 34.319 26.94
2012-01-09 00:00:00+00:00 339.522 87.342 NaN 34.323 27.21

#delete column
prices = prices.drop('TSLA', axis=1)
prices.head(5)
CMG MCD SHAK WFM
2012-01-03 00:00:00+00:00 340.980 86.631 NaN 32.788
2012-01-04 00:00:00+00:00 348.740 87.166 NaN 33.650
2012-01-05 00:00:00+00:00 349.990 87.526 NaN 34.257
2012-01-06 00:00:00+00:00 348.950 88.192 NaN 34.319
2012-01-09 00:00:00+00:00 339.522 87.342 NaN 34.323

#combine column
df_1 = get_pricing(['SPY', 'VXX'], start_date=start, end_date=end, fields='price')
df_2 = get_pricing(['MSFT', 'AAPL', 'GOOG'], start_date=start, end_date=end, fields='price')
df_3 = pd.concat([df_1, df_2], axis=1)
df_3.head()
Equity(8554 [SPY]) Equity(51653 [VXX]) Equity(5061 [MSFT]) Equity(24 [AAPL]) Equity(46631 [GOOG])
2012-01-03 00:00:00+00:00 118.414 NaN 23.997 54.684 NaN
2012-01-04 00:00:00+00:00 118.498 NaN 24.498 54.995 NaN
2012-01-05 00:00:00+00:00 118.850 NaN 24.749 55.597 NaN
2012-01-06 00:00:00+00:00 118.600 NaN 25.151 56.194 NaN
2012-01-09 00:00:00+00:00 118.795 NaN 24.811 56.098 NaN

quantopian lecture Pandas

import numpy as np
import pandas as pd
import matplotlib.pyplot as plt

#mean = 1, standard deviation = 0.03, 10 stocks, 100 samples/stock
returns = pd.DataFrame(np.random.normal(1, 0.03, (100, 10)))
#accumulative product of return
prices = returns.cumprod()
prices.plot()
plt.title('randomly generated prices')
plt.xlabel('time')
plt.ylabel('price')
plt.legend(loc=0)

s = pd.Series([1, 2, np.nan, 4, 5])
print s
print s.index

0    1.0
1    2.0
2    NaN
3    4.0
4    5.0
dtype: float64
RangeIndex(start=0, stop=5, step=1)

new_index = pd.date_range('2019-01-01', periods = 5, freq='D')
print new_index
s.index = new_index

DatetimeIndex(['2019-01-01', '2019-01-02', '2019-01-03', '2019-01-04',
               '2019-01-05'],
              dtype='datetime64[ns]', freq='D')

s.iloc[0]
s.iloc[len(s)-1]
s.iloc[:2]
s.iloc[0: len(s): 1]

2019-01-01    1.0
2019-01-02    2.0
2019-01-03    NaN
2019-01-04    4.0
2019-01-05    5.0
Freq: D, dtype: float64

s.iloc[::-1]

2019-01-05    5.0
2019-01-04    4.0
2019-01-03    NaN
2019-01-02    2.0
2019-01-01    1.0
Freq: -1D, dtype: float64

s.loc['2019-01-02':'2019-01-04']

2019-01-02    2.0
2019-01-03    NaN
2019-01-04    4.0
Freq: D, dtype: float64

#Boolean Indexing
print s < 3

2016-01-01     True
2016-01-02     True
2016-01-03    False
2016-01-04    False
2016-01-05    False
Freq: D, Name: Toy Series, dtype: bool

print s.loc[s < 3]

2016-01-01    1.0
2016-01-02    2.0
Freq: D, Name: Toy Series, dtype: float64

print s.loc[(s < 3) & (s > 1)]

2016-01-02    2.0
Freq: D, Name: Toy Series, dtype: float64

symbol = "CMG"
start = "2012-01-01"
end = "2016-01-01"
prices = get_pricing(symbol, start_date=start, end_date=end, fields="price")

print "\n", type(prices)
prices.head(5)

<class 'pandas.core.series.Series'>
2012-01-03 00:00:00+00:00    340.980
2012-01-04 00:00:00+00:00    348.740
2012-01-05 00:00:00+00:00    349.990
2012-01-06 00:00:00+00:00    348.950
2012-01-09 00:00:00+00:00    339.522
Freq: C, Name: Equity(28016 [CMG]), dtype: float64

monthly_prices = prices.resample('M').mean()
monthly_prices.head(10)

2012-01-31 00:00:00+00:00    354.812100
2012-02-29 00:00:00+00:00    379.582000
2012-03-31 00:00:00+00:00    406.996182
2012-04-30 00:00:00+00:00    422.818500
2012-05-31 00:00:00+00:00    405.811091
2012-06-30 00:00:00+00:00    403.068571
2012-07-31 00:00:00+00:00    353.849619
2012-08-31 00:00:00+00:00    294.516522
2012-09-30 00:00:00+00:00    326.566316
2012-10-31 00:00:00+00:00    276.545333
Freq: M, Name: Equity(28016 [CMG]), dtype: float64

monthly_prices_med = prices.resample('M').median()
monthly_prices_med.head(10)

2012-01-31 00:00:00+00:00    355.380
2012-02-29 00:00:00+00:00    378.295
2012-03-31 00:00:00+00:00    408.850
2012-04-30 00:00:00+00:00    420.900
2012-05-31 00:00:00+00:00    405.390
2012-06-30 00:00:00+00:00    402.790
2012-07-31 00:00:00+00:00    380.370
2012-08-31 00:00:00+00:00    295.380
2012-09-30 00:00:00+00:00    332.990
2012-10-31 00:00:00+00:00    286.440
Freq: M, Name: Equity(28016 [CMG]), dtype: float64

def custom_resampler(array_like):
    """ Returns the first value of the period """
    return array_like[0]

first_of_month_prices = prices.resample('M').apply(custom_resampler)
first_of_month_prices.head(10)

2012-01-31 00:00:00+00:00    340.98
2012-02-29 00:00:00+00:00    370.84
2012-03-31 00:00:00+00:00    394.58
2012-04-30 00:00:00+00:00    418.65
2012-05-31 00:00:00+00:00    419.78
2012-06-30 00:00:00+00:00    397.14
2012-07-31 00:00:00+00:00    382.97
2012-08-31 00:00:00+00:00    280.60
2012-09-30 00:00:00+00:00    285.91
2012-10-31 00:00:00+00:00    316.13
Freq: M, Name: Equity(28016 [CMG]), dtype: float64

#Missing Data
#fill in the missing days with the mean price of all days.
meanfilled_prices = calendar_prices.fillna(calendar_prices.mean())

#fill in the missing days with the next known value.
bfilled_prices = calendar_prices.fillna(method='bfill')

#drop missing data
dropped_prices = calendar_prices.dropna()

prices.plot();
# We still need to add the axis labels and title ourselves
plt.title(symbol + " Prices")
plt.ylabel("Price")
plt.xlabel("Date");

print "Summary Statistics"
print prices.describe()

Summary Statistics
count    1006.000000
mean      501.637439
std       146.697204
min       236.240000
25%       371.605000
50%       521.280000
75%       646.753750
max       757.770000
Name: Equity(28016 [CMG]), dtype: float64

#inject noise
noisy_prices = prices + 5 * pd.Series(np.random.normal(0, 5, len(prices)), index=prices.index) + 20
noisy_prices.plot();
plt.title(symbol + " Prices")
plt.ylabel("Price")
plt.xlabel("Date");

#first order differential 

add_returns = prices.diff()[1:]

add_returns.plot();
# We still need to add the axis labels and title ourselves
plt.title(symbol + " Prices 1st order diff")
plt.ylabel("Price diff")
plt.xlabel("Date");

#percent change( multiplicative returns)
percent_change = prices.pct_change()[1:]

plt.title("Multiplicative returns of " + symbol)
plt.xlabel("Date")
plt.ylabel("Percent Returns")
percent_change.plot();

#prices and multiplicative returns
ax1 = plt.subplot2grid((6, 1), (0, 0), rowspan=5, colspan=1)
ax2 = plt.subplot2grid((6, 1), (5, 0), rowspan=1, colspan=1, sharex=ax1)

ax1.plot(prices.index, prices)
ax2.plot(percent_change.index, percent_change)

#30 day rolling mean
rolling_mean = prices.rolling(window=30,center=False).mean()
rolling_mean.name = "30-day rolling mean"

prices.plot()
rolling_mean.plot()
plt.title(symbol + "Price")
plt.xlabel("Date")
plt.ylabel("Price")
plt.legend();

路易吉洋樓3

quantopian lecture NumPy

import numpy as np
import matplotlib.pyplot as plt

A = np.array([[1, 2], [3, 4]])
print A, type(A)
print A.shape
#first column
print A[:, 0]
#first row
print A[0, :]
#first row
print A[0]
#second row, second column
print A[1, 1]

------------------------
[[1 2]
 [3 4]] <type 'numpy.ndarray'>
(2, 2)
[1 3]
[1 2]
[1 2]
4

-----------------------------
stock_list = [3.5, 5, 2, 8, 4.2]
returns = np.array(stock_list)
print returns, type(returns)
print np.log(returns)
print np.mean(returns)
print np.max(returns)
returns*2 + 5
print "Mean: ", np.mean(returns), "Std Dev: ", np.std(returns)

---------------------------------
[ 3.5  5.   2.   8.   4.2] <type 'numpy.ndarray'>
[ 1.25276297  1.60943791  0.69314718  2.07944154  1.43508453]
4.54
8.0
Mean:  4.54 Std Dev:  1.99158228552

------------------------------------
N = 10
#create matrix with N rows, 20 columns, all values 0
returns = np.zeros((N, 20))

#generate 20 values (1+-0.1) for each of 10 stocks to simulate 10% fluctuation
for i in range(0, N):
    returns[i] = np.random.normal(1, 0.1, 20)

print returns

-------------------
[[ 1.03106776  1.05468042  0.95484129  1.00791592  0.97503239  1.16924021
   1.03094272  0.88663418  0.98184415  1.12563429  1.10268922  1.04089233
   0.89611761  0.96677619  0.96622677  0.91201808  1.00382794  1.1401533
   0.98819255  1.14371201]
 [ 0.78958078  1.05885922  0.86220874  0.89660524  0.98059216  0.87783413
   0.90657333  1.03980406  1.06212268  0.92187714  0.96084574  0.99757358
   0.89130947  0.98494642  0.98927777  1.07842667  0.89442444  1.01049714
   0.84995483  1.0591395 ]
 [ 1.22490492  0.96571626  1.00179064  1.0928795   1.04838166  0.91973272
   0.97177359  0.91569413  1.17500945  1.14197296  1.10279227  1.01789198
   1.0679357   1.02915363  1.0061314   1.06420138  1.0345859   1.03125553
   0.86506542  1.07629615]
 [ 0.98187678  0.87289137  0.89466529  0.95013111  1.02461151  0.99680892
   0.91350208  0.88012537  0.85386131  0.9482019   0.93380868  0.91333927
   0.94250097  1.15446     1.13059652  1.20503639  0.90927665  0.85362986
   1.14138124  1.06879598]
 [ 1.07101098  0.96595767  1.06083827  1.16424979  0.95199777  1.03350921
   0.98425205  1.01869927  0.93129452  1.02147242  0.97701336  0.97043075
   1.17036581  1.06068463  1.15400094  1.01938223  1.08851357  1.13253319
   1.06476737  1.19244557]
 [ 1.05019664  0.97590288  1.0830167   1.00392006  1.07881173  1.07049307
   1.17038075  0.95942305  0.7484157   1.05945289  1.07379404  1.0268822
   1.0217178   0.9949103   1.05066957  0.74864275  1.06412451  0.961283
   0.87042728  1.07378468]
 [ 0.89085125  1.10119192  1.00990661  0.91820266  1.00908679  0.73740874
   1.00485464  0.97427282  1.09424579  0.84876444  1.01691899  1.0188415
   1.15582724  0.90586819  0.87907785  1.05440651  0.92476789  0.87475955
   1.09272491  0.93802951]
 [ 0.97633747  1.21554237  0.95190964  1.0345212   1.0123711   1.03702179
   1.11903298  0.90348583  0.97683806  0.87895557  0.92125309  1.0532206
   0.95497304  1.11988127  1.1355286   1.07307923  0.97733744  1.08540676
   0.97249376  0.89770286]
 [ 1.08621875  1.0198653   1.04726792  0.98290847  1.05640872  0.89579798
   1.09843927  0.83548153  1.02303315  0.90011522  0.96444887  1.26715629
   1.14621686  0.98682604  0.97082908  1.06998541  1.15237376  1.03912552
   0.87601541  0.84186623]
 [ 1.00719248  0.98842068  0.92611714  0.89175453  1.02358354  0.98464005
   1.16993698  0.89091489  1.00820166  1.07533476  1.06151955  0.8967124
   0.93210651  1.02820371  1.01284052  0.94901959  0.85795195  1.05141096
   0.99480577  0.80594927]]
 
 ---------------------------
 #mean percentage returns of stocks
mean_returns = [(np.mean(R) - 1)*100 for R in returns]
print mean_returns

plt.bar(np.arange(N), mean_returns)
plt.xlabel('Stock')
plt.ylabel('Returns')
plt.title('Returns for {0} Random Assets'.format(N));

----------------------------------
[1.8921966974847049, -4.4377348109003512, 3.7658259559407714, -2.1524940254945335, 5.1670968189016619, 0.43124796965616774, -2.7499609644974221, 1.4844633385441064, 1.3018988447207835, -2.2169154058116147]

---------------------
#simulate portfolio of 10 stocks
weights = np.random.uniform(0, 1, N)
weights = weights/np.sum(weights)
print weights

---------------------
[ 0.18746564  0.13005439  0.13909044  0.00896143  0.27201674  0.0756121
  0.10938963  0.02699273  0.03911474  0.01130216]

-----------------------
#calculate portfolio return
#np.dot(a, b) = a1b1 + a2b2 + a3b3 ...
p_returns = np.dot(weights, mean_returns)
print "Expected return of the portfolio: ", p_returns

-------------------------
Expected return of the portfolio:  1.48534036925

--------------------------
v = np.array([1, 2, np.nan, 4, 5])
print np.mean(v)
ix = ~np.isnan(v)
print ix
print v[ix]
print np.mean(v[ix])
#calculate nonnull mean
print np.nanmean(v)

---------------------------
nan
[ True  True False  True  True]
[ 1.  2.  4.  5.]
3.0
3.0

-------------------------------
A = np.array([
        [1, 2, 3, 12, 6],
        [4, 5, 6, 15, 20],
        [7, 8, 9, 10, 10]       
    ])
B = np.array([
        [4, 4, 2],
        [2, 3, 1],
        [6, 5, 8],
        [9, 9, 9]
    ])
print np.dot(B, A)
print np.transpose(A)

-------------------
[[ 34  44  54 128 124]
 [ 21  27  33  79  82]
 [ 82 101 120 227 216]
 [108 135 162 333 324]]
[[ 1  4  7]
 [ 2  5  8]
 [ 3  6  9]
 [12 15 10]
 [ 6 20 10]]

https://www.quantopian.com/lectures/introduction-to-numpy

quantopian lecture introduction to python

https://www.quantopian.com/lectures/introduction-to-python

微信和支付宝开放绑定加拿大信用卡

近几年回过国的加拿大华人，一定感受过国内出门不用带现金的便利，小到地摊上5块钱一个的煎饼果子，大到几百万一套的房子，都可以用手机直接付款。更不用说，微信支付、支付宝整天琢磨着抢客户，所以各种优惠减免层出不穷：去趟超市买了300块的东西，一扫微信支付，立减200；去吃个火锅消费500，一扫支付宝，喜提免单。

然而，这种一个手机行天下的便利和薅羊毛的幸福只属于国内的小伙伴们，与海外华人无关。有时候回了国想赶时髦用用手机支付，却发现自己被“没有中国身份证认证”，或者“没有中国的借记卡关联”挡在门外，所以每次都得提前把加元现金换成人民币带回国用。不过，现在好消息来了！中国经济网11月7日发布重磅消息：支付宝和微信支付全面升级，支持绑定境外银行卡，向境外华人敞开大门！中国经济网指出，不能便捷地使用移动支付，已成为海外华人在中国生活的一大痛点。近日，支付宝、微信支付两大移动支付巨头宣布全面向境外持卡人开放，由此来华外籍人士可便利使用移动支付。腾讯公司在相关政策指引下，与Visa、Mastercard、AmericanExpress、Discover Global Network（含Diners Club）、JCB五大国际卡组织开展一系列合作，支持境外开立的国际信用卡绑定微信支付，以支持用户在12306购票、滴滴出行、京东、携程等覆盖衣食住行的数十个商户消费，后续将在监管指导下、在严格落实反洗钱相关政策基础上，进一步有序放开更多使用场景。境外用户认证时需要的证件：护照、港澳回乡证、台胞证、港澳居民居住证和台湾居民居住证中的任一证件开立储蓄卡及信用卡，绑定后即可使用微信支付进行线上、线下的多场景消费。在微信支付中绑定国际信用卡有两种方法，一种是在付款时绑定，一种是提前绑定。付款时绑定的步骤第一步：扫描付款码，第二步：确认付款，第三步：添加一张国际信用卡，第四步：付款成功。其中第三步绑定国际信用卡时，需要填写信用卡信息，包括卡号、过期日期、CVV码以及持卡人的姓名、住址、电话等。如果暂时不买东西，也可以提前绑定，方便以后的不时之需。提前绑定的步骤第一步：点击微信支付中的“钱包”，第二步：点击“银行卡”，第三步：添加新银行卡，点击相机图标，对着需要绑定的银行卡拍照，第四步：填写信用卡信息，绑定成功。另外，就在上个月，腾讯还为推出了We TaxFree Pass微信小程序，方便入境游客在离境时使用微信退税。这一新政不光将便利回国的加拿大华人，对温哥华的华人小伙伴来说，更是大好消息。目前，大温各个城市各类商家，都陆续开始了支付宝、微信扫码付款服务，只不过之前，温村村民们用的都是国内银行卡里的钱，现在，可以直接绑定加拿大本地银行卡进行微信、支付宝付款啦！
https://www.bcbay.com/news/2019/11/13/664994.html

python quantopian 3 schedule, benchmark

algorithm trade lose holding stock (not trading) by 28%

def initialize(context):
    #performance for holding stock without trade
    set_benchmark(sid(24))
    context.aapl = sid(24)
    #schedule function fires everyday after market open 1h instead of default every minute.
    #up side: faster analysis, fewer trades, downside poor return.    
    schedule_function(ma_crossover_handling, date_rules.every_day(), time_rules.market_open(hours=1))
 
def ma_crossover_handling(context, data):
    hist = data.history(context.aapl, 'price', 50, '1d')
    log.info(hist)
    sma_50 = hist.mean()
    sma_20 = hist[-20:].mean()
 
    if sma_20 > sma_50:
       order_target_percent(context.aapl, 1.0)
         
    elif sma_50 > sma_20:
       order_target_percent(context.aapl, -1.0)

The British Property Boom

https://www.numbeo.com/cost-of-living/compare_cities.jsp?country1=Canada&country2=United+Kingdom&city1=Calgary&city2=London&tracking=getDispatchComparison

python quantopian 2 buy & sell

simulate trade performance based on python algorithm

def initialize(context):

    context.aapl = sid(24)

    

def handle_data(context, data):

    hist = data.history(context.aapl, 'price', 50, '1d')

    log.info(hist)

    #last 50 day average

    sma_50 = hist.mean()

    #last 20 day average

    sma_20 = hist[-20:].mean()

    

    if sma_20 > sma_50:

       #buy apple with all money

       order_target_percent(context.aapl, 1.0)

           

    elif sma_50 > sma_20:

       #sell all apple share

       order_target_percent(context.aapl, -1.0)

reference:

https://www.youtube.com/watch?v=H5LLJDJ3jTI&list=PLQVvvaa0QuDcOdF96TBtRtuQksErCEBYZ&index=14

World's CRAZIEST Meal - Alchemist Mark Wiens

python quantopian 1 get stock price

Quantopian https://www.quantopian.com/ -> Research -> Algorithm -> change Start date 10/01/2019 End date 11/01/2019 -> save - > build algorithm

def initialize(context):
    context.aapl = sid(24)
   
def handle_data(context, data):
    #get apple stock price history data array, array consists data samples every minute from start to end date. Each data has 10 samples. 1 sample every day.
    hist = data.history(context.aapl, 'price', 10, '1d')
    log.info(hist)

umidigi f2 11.11 sale

https://www.aliexpress.com/item/4000178715895.html?spm=a2g0s.9042311.0.0.14734c4dnjP9I0